Preliminaries
An additional U(1)D gauge symmetry added to the SM is theoretically well-motivated and occurs in many top-down and bottom-up extensions of the SM. The U(1)D vector boson (the "dark photon" or the "dark-Z") is usually referred to as A′, Z′, γD, or ZD in the literature and various possibilities exist to connect the additional U(1)D to the SM (see e.g. [1,2,3,4] for reviews). The U(1)D can couple to the SM sector via a small gauge kinetic mixing term [1/2] ϵF′μν Bμν [5,6,7] between the dark photon and the hypercharge gauge boson. This renormalizable interaction can be generated at a high scale in a grand unified theory or in the context of string theory with a wide range of ϵ ∼ 10−17 − 10−2. This term effectively gives SM matter a dark milli-charge and allows for dark photon decay to SM particles and possible experimental detection. To avoid the tight constraints on new long-range forces, a `dark Higgs' S with a non-zero vacuum expectation value can give a non-zero mass to the A′. An A′ with a sub-GeV mass can be probed at beam dumps and colliders, and with measurements of the muon anomalous magnetic moment, supernova cooling, and rare meson decays, see Fig. 1 and e.g. [4] for a recent review. A broken U(1)D can also lead to exotic Higgs decays, especially if there is mixing between the two Higgs sectors. In this context we refer to the corresponding vector field as ZD. The possibility of h → ZD ZD through Higgs-to-dark-Higgs mixing or h → Z ZD through Z-ZD mass mixing (which is also induced by the above-mentioned kinetic mixing) was discussed in [8] and [9,10], respectively, with both occurring, for example, in hidden valley models [11,12]. To examine the range of possible exotic Higgs phenomena due to a U(1)D sector we examine the model of [8], but with mh set to 125 GeV and allowing for the full range of dark Higgs and dark-Z masses relevant to exotic Higgs decay phenomenology.1 This includes Higgs-to-dark-Higgs mixing and kinetic mixing between the B boson and the dark vector ZD, but no explicit mass mixing between the Z and ZD.2 We will assume prompt ZD decays, which requires mZD >~10 MeV given the current constraints shown in Fig. 1.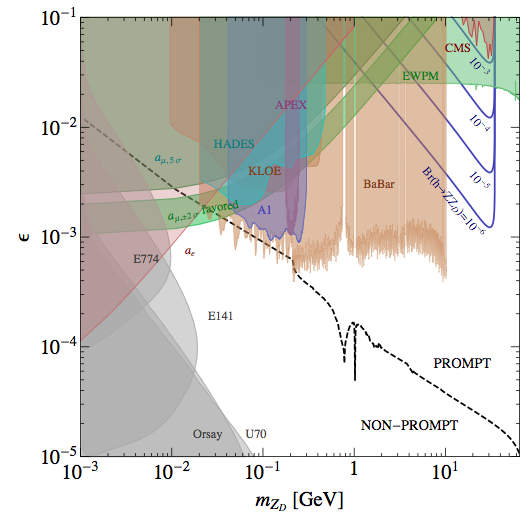
Figure 1: Constraints on ϵ, mZD for pure kinetic mixing (no additional source of Z-ZD mass mixing) for mZD ∼ MeV-10 GeV. The black dashed line separates prompt (cτ < 1 μm) from non-prompt decays. The three blue lines are contours of Br(h → Z ZD) of 10−4, 10−5, 10−6 respectively. Shaded regions are existing experimental constraints, see e.g. [4] for a recent review.
Model Details
The model is defined by a U(1)D gauge sector and a SM singlet S that has unit charge under the U(1)D. The kinetic terms of the hypercharge and U(1)D gauge bosons (adopting mostly the notation of [9]) are
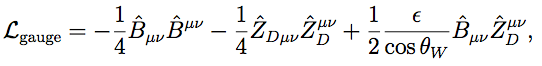 (1)
(1)
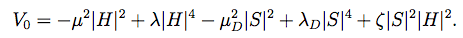 (2)
(2)
 (3)
(3)

Figure 2:
(a) Branching ratios for ZD decay, to lowest order and without QCD corrections, assuming decays to the dark sector are kinematically forbidden. l stands for either e or μ. Hadronization effects likely invalidate our simple calculation in the shaded region. (b) Branching ratios for ZD decay for mZD <~3 GeV, including non-perturbative QCD effects.
The Higgs potential is minimized by vacuum expectation values of H0 and S
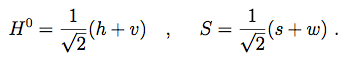 (4)
(4)
 (5)
(5)
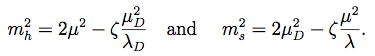 (6)
(6)
 Figure 3: The dominant exotic Higgs decays in the SM+V model. The h → Z ZD matrix element is proportional to the gauge kinetic mixing ϵ, while h → ZD ZD and h → s s are controlled by the Higgs mixing parameter ζ. The vertex h s ZD is present but suppressed by both mixings.
Figure 3: The dominant exotic Higgs decays in the SM+V model. The h → Z ZD matrix element is proportional to the gauge kinetic mixing ϵ, while h → ZD ZD and h → s s are controlled by the Higgs mixing parameter ζ. The vertex h s ZD is present but suppressed by both mixings.- Gauge mixing dominates:For ϵ >> ζ the dominant exotic Higgs decay is h → Z ZD. To leading order in mZD2/mZ2 the partial width is
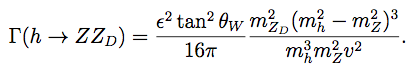 (7)
(7)
- Higgs mixing dominates:When ζ >> ϵ and Higgs mixing dominates then h → ZD ZD, s s are both possible, depending on the spectrum of the dark sector. (We still assume that ϵ is large enough for ZD to decay promptly.) The partial decay widths to leading order in ζ are
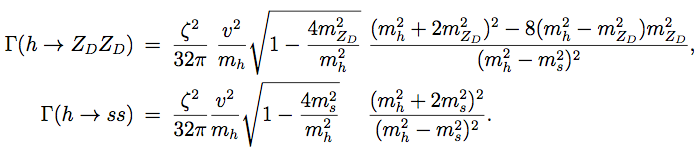 (8)
(8)
- Intermediate Regime:Here the decays induced by kinetic and Higgs mixing are comparable. For example, Figure 1 shows that ϵ ∼ 10−2 is not excluded for some values of mZD, allowing Br(h→ Z ZD) ∼ 10−4. The branching ratios for h→ ZD ZD, s s will be similar if ζ ∼ 10−4.
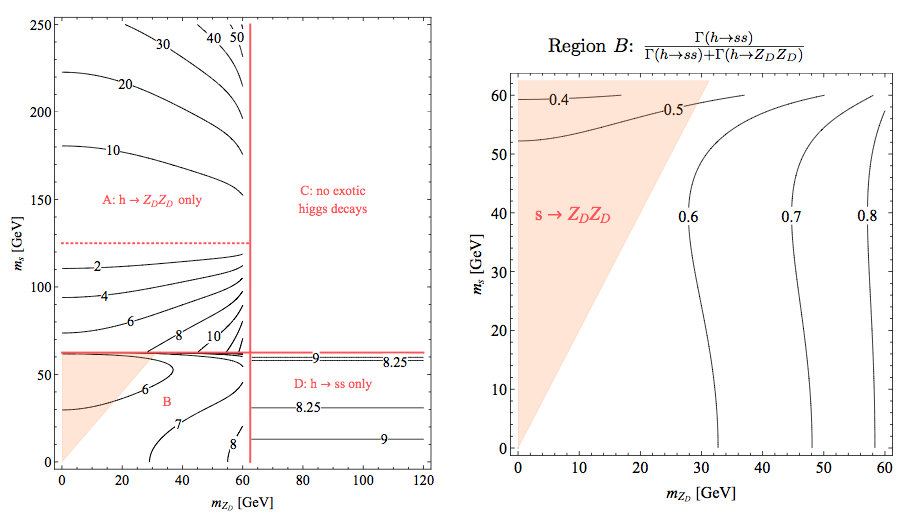
Figure 4: Left: Regions of the (mZD, ms) mass plane in the SM+V model with different exotic Higgs decays for ζ >> ϵ (i.e. when the mixing between the Higgs and dark-Higgs dominates over the kinetic mixing). The black contours are the values of ζ×103 required for Br(h → ZD ZD, s s) = 10%. Region A is the case examined by [8] (the dotted red line indicates mh = ms). Region C has no exotic Higgs decays. Region D reproduces the SM+S model. Region B has both h → s s and h → ZD ZD decays, with the h → ss fraction of exotic decays shown on the right. In the upper left shaded region, s → ZD ZD is the dominant decay mode of the dark scalar. This allows the Higgs to decay to up to 8 SM fermions.
Summary
In summary, the SM+V setup allows for many different kinds of exotic Higgs decays, including h → Z ZD, h→ ZD ZD, and h→ ss, with ZD → f―f , and s → f―f or s → ZD ZD → (f―f)(f―f). This leads to final states of Z + (f―f), (f―f)(f―f), and ((f―f)(f―f))((f―f)(f―f)), where parentheses around a set of particles denotes a resonance (all final-state particles combined will form the Higgs resonance). Since the ZD (although not the s) couples to the fermions' gauge charges, final states with several light leptons have sizable branching fractions over the entire kinematically permitted mass range. Certain spectra can produce interesting lepton-jet signatures.MadGraph Model
MadGraph Model
We have constructed a validated MadGraph 5 model for the SM + vector + dark higgs scenario outlined here. This can be used for signal generation in experimental and phenomenological studies.
Link to MadGraph5 model for SM + S + V
Branching Ratio Tables
In "Illuminating Dark Photons with High-Energy Colliders" (Curtin, Essig, Gori, Shelton, arXiv:1412.0018) we compute the dark photon total width and branching ratio to leptons Br(ZD->ll) including QCD corrections, using PDG experimental data for mZD < 12 GeV, and by repurposing the calculations of hep-ph/0005139 for mZD > 12 GeV. We also compute the exotic higgs decay branching ratios Br(h->ZdZ*->4l) and Br(h->ZdZd->4l). All of these computed widths and branching ratios can be downloaded as a text table here. (See 1412.0018 for more details.)References
[1]P. Langacker, The Physics of Heavy Z′ Gauge Bosons, Rev.Mod.Phys. 81 (2009) 1199-1228, [arXiv:0801.1345].
[2]J. Jaeckel and A. Ringwald, The Low-Energy Frontier of Particle Physics, Ann.Rev.Nucl.Part.Sci. 60 (2010) 405-437, [arXiv:1002.0329].
[3]J. Hewett, H. Weerts, R. Brock, J. Butler, B. Casey, et. al., Fundamental Physics at the Intensity Frontier, [arXiv:1205.2671].
[4]R. Essig, J. A. Jaros, W. Wester, et. al., Dark Sectors and New, Light, Weakly-Coupled Particles, [arXiv:1311.0029].
[5]B. Holdom, Two U(1)'s and Epsilon Charge Shifts, Phys.Lett. B166 (1986) 196.
[6]P. Galison and A. Manohar, TWO Z's OR NOT TWO Z's?, Phys.Lett. B136 (1984) 279.
[7]K. R. Dienes, C. F. Kolda, and J. March-Russell, Kinetic mixing and the supersymmetric gauge hierarchy, Nucl.Phys. B492 (1997) 104-118, [ hep-ph/9610479].
[8]S. Gopalakrishna, S. Jung, and J. D. Wells, Higgs boson decays to four fermions through an abelian hidden sector, Phys.Rev. D78 (2008) 055002, [arXiv:0801.3456].
[9]H. Davoudiasl, H.-S. Lee, and W. J. Marciano, 'Dark' Z implications for Parity Violation, Rare Meson Decays, and Higgs Physics, Phys.Rev. D85 (2012) 115019, [arXiv:1203.2947].
[10]H. Davoudiasl, H.-S. Lee, I. Lewis, and W. J. Marciano, Higgs Decays as a Window into the Dark Sector, [ arXiv:1304.4935].
[11]M. J. Strassler, Why Unparticle Models with Mass Gaps are Examples of Hidden Valleys, [ arXiv:0801.0629].
[12]M. J. Strassler and K. M. Zurek, Echoes of a hidden valley at hadron colliders, Phys.Lett. B651 (2007) 374-379, [hep-ph/0604261].
[13]C.-F. Chang, E. Ma, and T.-C. Yuan, Multilepton Higgs Decays through the Dark Portal, [ arXiv:1308.6071].
[14]Particle Data Group, J. Beringer et. al., Review of Particle Physics (RPP), Phys.Rev. D86 (2012) 010001.
[15]N. Arkani-Hamed and N. Weiner, LHC Signals for a SuperUnified Theory of Dark Matter, JHEP 0812 (2008) 104, [arXiv:0810.0714].
File translated from TEX by TTH, version 4.03. On 17 Dec 2013, 16:29.
Footnotes:
1Ref. [13] appeared while this work was being completed, performing a similar analysis with a different focus on constraining the couplings of the extended Higgs potential for relatively low mZD < 5 GeV. 2The constraints shown in Fig. 1 are altered in the presence of such pure mass mixing, which requires additional Higgs doublets that also carry dark charge. The resulting ZD → SM decays would be more Z-like and lead to additional constraints from rare meson decays as well as new parity-violating interactions [9]. However, we stress that the exotic Higgs phenomenology would not be qualitatively different.File translated from TEX by TTH, version 4.03. On 17 Dec 2013, 16:29.