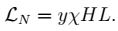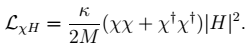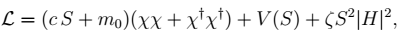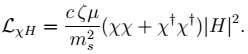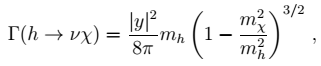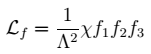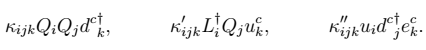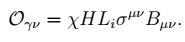We here discuss exotic Higgs decays that can arise by the addition of a light fermion to the SM. We focus on two possibilities,
neutrino portal-mediated and
Higgs portal-mediated Higgs decays.
The leading interaction of a single Majorana fermion χ with the SM fields is given by the renormalizable but lepton-number violating "neutrino portal" operator,
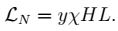 |
(1) |
If this lepton-number violating coupling is forbidden, the leading coupling between χ and the SM is through the dimension five Higgs portal operator
1,
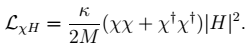 |
(2) |
This kind of coupling occurs, for instance, in the MSSM when all BSM degrees of freedom except a bino-like neutralino are integrated out at a high scale. In the MSSM, the states integrated out to generate this operator are fermionic, with electroweak quantum numbers. In UV completions where the state being integrated out is bosonic, the operator of Eq. (
2) has effective coupling [(μ)/(2
M2)], where μ is some hidden sector mass scale. This is a consequence of chiral symmetry, and, as we frequently may have μ <<
M, may result in the Higgs portal interaction becoming effective dimension six. As an example of this kind of UV completion, consider a simple hidden sector consisting of a singlet scalar
S together with the fermion χ,
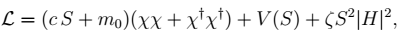 |
(3) |
and let
V(
S) allow
S to develop a vacuum expectation value, 〈
S 〉 ≡ μ.
2 Then integrating out the excitations of
S around this 〈
S 〉, with mass
ms, we obtain the operator
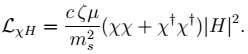 |
(4) |
The mass of the fermion is
mχ =
m0+
cμ, so either there are large cancellations or
cμ ∼
m0 ∼
mχ <<
ms, and the operator is effective dimension-six.
Neutrino portal-mediated Higgs decays
We first consider exotic Higgs decays mediated by the neutrino portal operator, Eq. (
1). The renormalizable neutrino portal coupling occurs in the so-called νSM, the minimal model that can give mass to the SM neutrinos. Here the SM is extended by sterile neutrinos, allowing the SM neutrinos to get a mass from a see-saw type mechanism triggered by a Majorana mass term (
M/2) χχ. The operator of Eq. (
1) mixes the sterile neutrino χ with the active SM neutrino ν arising from the
SU(2) doublet
L. In the absence of large cancellations in the neutrino mass matrix, sterile neutrinos must be extremely heavy,
M >>
v, or extremely decoupled,
y <<
ye << 1. In this limit, the decay
h→χν is negligible, even if kinematically allowed. However, the authors of [
1,
2] show that active-sterile mixing angles as large as several percent are possible, with (accidental) cancellations among the Yukawa couplings still allowing for small active neutrino masses. Mixing angles of the order of a few percent may imply a sizable partial width for
h→νχ,
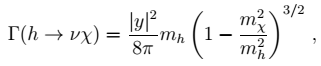 |
(5) |
where
mχ is the mass of the sterile neutrino χ. For
mh < 130 GeV, neutrino data and pion decay constraints on W-lepton coupling universality still allow the partial width into
h→νχ to exceed that into
h→
bb, see [
2] for a detailed discussion (see also [
3]).
The mass mixing between sterile (right-handed (RH)) neutrinos and active (left-handed (LH)) neutrinos introduces couplings of the RH neutrinos to
W and
Z gauge bosons. Therefore, in the region of parameter space for which the active-sterile mixing angle Θ is close to its phenomenological upper bound, the RH neutrinos decay promptly into χ→
lW*→
lf f′ and χ→ ν
Z*→ ν
ff, where
f and
f′ are either a lepton or a quark of the SM, and with all branching ratios fixed by the electroweak quantum numbers of the SM fermions. In general χ may have non-zero mixings with one, two, or all three SM neutrinos.
Higgs portal-mediated Higgs decays
We next turn to the higher-dimension decays, mediated by the higher-dimension operator of Eq. (
2). After electroweak symmetry breaking, this operator yields a coupling λ
h(χχ+ χ
†χ
†), with effective Yukawa coupling given by λ = κ
v/2
M. The resulting partial width into χ is then
 |
(6) |
As the effective Yukawa coupling λ is only competing with the small
b-quark Yukawa, substantial branching fractions Br(
h→χχ) can be obtained even for Higgs portal scales
M significantly above a TeV, as shown in Fig.
1, where we fix κ = 1 for simplicity.
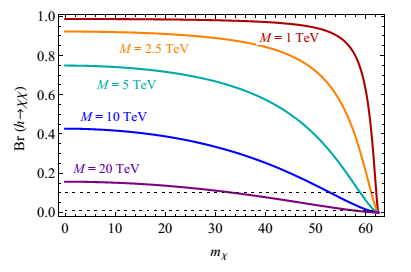
Figure 1:
Higgs branching fraction into Majorana fermions χ resulting from the partial width of Eq. (6), as a function of the Higgs portal scale M and the mass of the fermion mχ. We fix the coupling κ to be equal to 1. Dotted lines indicate branching ratios of 0.1 and 0.01.
The kinds of signatures that are realized depends on how χ decays. If the Higgs portal coupling of Eq. (
2) is the only interaction that the new fermion χ possesses, then χ is absolutely stable, and the resulting Higgs decay is invisible. In general, however, χ will possess additional interactions. If these interactions preserve the
Z2 symmetry taking χ→−χ, then χ will remain stable. On the other hand, if the
Z2 is violated by a dimension-six operator of the form
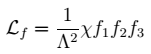 |
(7) |
where
f1f2f3 is a gauge-invariant combination of quarks and leptons, then χ will undergo the three-body decay χ→
f1f2f3. Some of these decays are familiar from previous study of R-parity violating neutralino decays in the MSSM, namely those involving holomorphic combinations of SM fermion fields (we suppress spinor structures for simplicity),
 |
(8) |
One may also consider the non-holomorphic operators [
4]
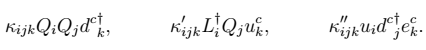 |
(9) |
Another flavor-violating possibility appearing at dimension six is the radiative decay χ→ γν, mediated by
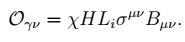 |
(10) |
While this operator can yield two-body final states, it naturally scales with a loop factor. All of these lepton and/or baryon-number violating decays necessarily have nontrivial flavor structure, and the combinations of operators that appear depends on the flavor structure of the UV theory. Unlike the SM plus scalar interactions considered in
SM+S and
2HDM+S or the neutrino-portal decays discussed earlier, the possible decays of χ are not determined by the Higgs coupling to the fermion, but require additional interactions, involving the flavor structure of the theory.
To summarize, the exotic Higgs signatures from a single additional (Majorana) fermion species are then Higgs decays to either invisible particles, or to one or more four- or six-body final states, where the six bodies form two three-body resonances of equal mass. When neutrinos are among the final state partons, the final states will include missing energy, and the resonances will not be reconstructable. This is always the case in the possible four-body final states where neutrinos are always involved, and is sometimes the case in the six-body final states.
References
- [1]J. Kersten and A. Y. Smirnov, Right-Handed Neutrinos at CERN LHC and the Mechanism of Neutrino Mass Generation, Phys.Rev. D76 (2007) 073005, [arXiv:0705.3221].
- [2]A. de Gouvea, GeV seesaw, accidentally small neutrino masses, and Higgs decays to neutrinos, [arXiv:0706.1732].
- [3]S. Chang and N. Weiner, Nonstandard Higgs decays with visible and missing energy, JHEP 0805 (2008) 074, [arXiv:0710.4591].
- [4]C. Csaki, E. Kuflik, and T. Volansky, Dynamical R-Parity Violation, [arXiv:1309.5957].
Footnotes:
1The dipole operator χ
†σ
μνχ
Fμν is also dimension five, but vanishes for a Majorana χ.
2For simplicity, we do not consider the possible interaction
S|
H|
2. This operator could be forbidden in the presence of a global symmetry taking
S→ −
S, χ→
iχ, which would also forbid the mass term
m0 (χχ+χ
† χ
† ).
File translated from TEX by TTH, version 4.03. On 17 Dec 2013, 23:45.