The Model
A particularly simple extension of the SM is to add to it one real scalar singlet S. This model can easily produce non-trivial exotic Higgs decays, since 1.) the Higgs can decay to pair of singlets; and 2.) the singlet decays to SM particles A simple model that could be conceived involves an additional real singlet added to the SM. At the renormalizable level, gauge invariance allows the singlet S to couple only to itself and to H† H ≡ |H|2. The resulting potential is given by![]()
Phenomenology
After electroweak symmetry breaking there are two relevant mass-eigenstates: the SM-like scalar h at 125 GeV containing a small admixture of S, and the mostly-singlet scalar s containing a small admixture of H. The phenomenology of any SM+S model can be, generally speaking, captured in terms of three parameters:- The effective Lagrangian contains a term of the form μv h s s, which gives h → s s with BR(h→ exotic) determined by μv.
- The singlet's mass ms affects BR(h→ exotic) and the type of SM final states available for s → SM.
- The mixing angle between S and H, denoted here by θS, determines the overall width of s→SM. If s cannot decay to other non-SM fields, θS controls its lifetime.
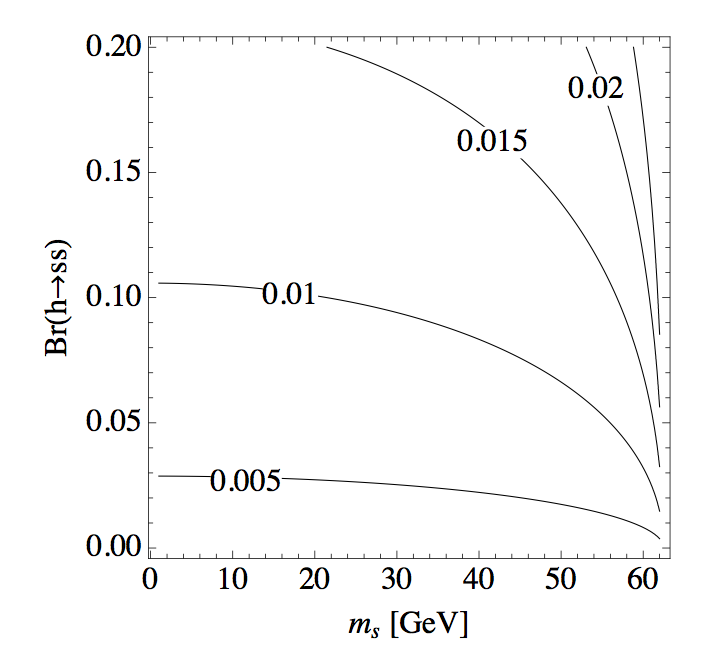
Figure 1: Size of the cubic coupling μv in units of Higgs expectation value v to yield the indicated h → s s branching fraction as a function of singlet mass.
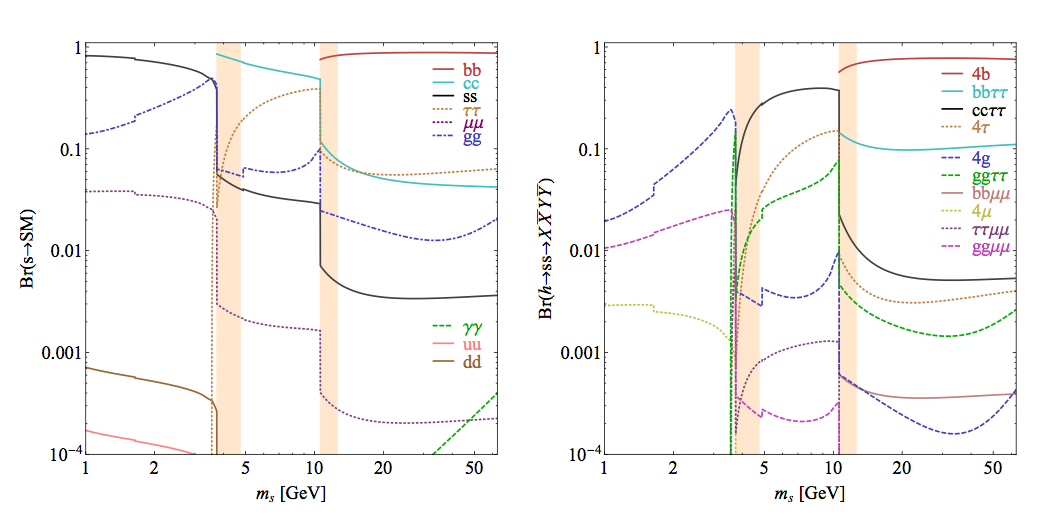
| Figure 2 (left) | Figure 2 (right) |
Figure 2: Left: Branching ratios of a CP-even scalar singlet to SM particles, as function of ms. Right: Branching ratios of exotic decays of the 125 GeV Higgs boson as function of ms, in the SM + Scalar model described in the text, scaled to BR(h→ ss) = 1. Hadronization effects likely invalidate our simple calculation in the shaded regions.
It should be pointed out that the partial decay widths are affected by the parity of s, however, the BR of s decaying to SM particles remains unchanged. Further, the decay width of s is suppressed by a factor of sin2 θs which opens the possibility of displaced vertices for θ <~10−6. Further details of the branching ratio calculation can be found in Section 1.3.2 and Appendix A of arXiv:1312.4992, which also includes a more detailed discussion of pseudoscalar decays.
MadGraph Model
We have constructed a validated MadGraph 5 model for the SM + vector + dark higgs scenario outlined here. Taking kinetic mixing to zero reduces this model to the SM+S scenario of this section. This can be used for signal generation in experimental and phenomenological studies.References
- [1]LHC New Physics Working Group, D. Alves et. al., Simplified Models for LHC New Physics Searches, J.Phys. G39 (2012) 105005, [arXiv:1105.2838].
- [2]A. Djouadi, The Anatomy of Electro-Weak Symmetry Breaking. II: The Higgs bosons in the Minimal Supersymmetric Model, [hep-ph/0503173v2].
- [3]A. Djouadi, The Anatomy of Electro-Weak Symmetry Breaking. I: The Higgs boson in the Standard Model, [hep-ph/0503172v2].
- [4]J. Gunion, H. Haber, G. Kane, and S. Dawson, The Higgs Hunter's Guide. Frontiers in Physics, V. 80. Perseus Pub., 2000.
File translated from TEX by TTH, version 4.03. On 12 Dec 2013, 14:20.