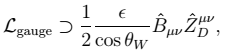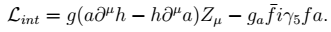Contact Person(s)
David Curtin, Rouven Essig, Zhen Liu, and Ze'ev Surujon
More details on this mode may be found in Section 10 of
Survey of Exotic Higgs Decays (
arXiv:1312.4992).
Theoretical Motivation
h→
ZZD
As discussed in
SM+V, many theories feature a hidden
U(1) sector with small kinetic or mass mixing the the SM photon and
Z-boson. This possibility often arises in connection to dark matter, but similar phenomenology can also arise in hidden valley models, see
Hidden Valley. The minimal setup to generate
h →
Z ZD decay involves a kinetic mixing term between the hypercharge gauge boson and the dark
U(1) gauge boson
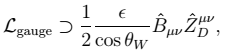 |
(1) |
where hatted quantities are fields before their kinetic terms are canonically renormalized by a shift of
Bμ. In the canonical basis, SM matter has dark milli-charge and there is mass mixing between the SM
Z-boson and
ZD. The dominantly dark vector mass eigenstate has photon-like couplings to SM fermions (proportional to the small mixing ϵ) up to
O(
mZD2/
mZ2) corrections.
It is also possible to have pure mass mixing after EWSB via operators of the form
h Zμ Z′
μ, but in this case additional constraints from parity violating interactions and rare meson decays apply, see [
1,
2,
3]. Generically, new physics similar to that which generates kinetic mixing may also generate dimension-6 terms of the form
H† HBμνZDμν/Λ
2. Once the Higgs acquires a VEV, this term yields the coupling in Eq. (
1).
h→
Za
Next we consider the decay
h→
Z a. This is motivated by, for example, by the
2HDM+S or the
NMSSM, where one of the CP-odd Higgs masses can be small. The relevant interaction Lagrangian in terms of mass eigenstates
h and
a is with an Yukawa term:
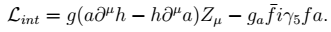 |
(2) |
with
g = √{(
g2+
g′
2)/2} sin(α− β) sinθ
a. α is the mixing angle between the doublet scalars, tanβ =
vu/
vd and θ
a is the mixing angle between the uneaten doublet pseudoscalar
A and the singlet pseudoscalar. Since the higgs coupling to
ZZ and
W+ W− is also proportional to sin(α− β), the SM-like rates in those channels (as well as the diphoton mode) favor the decoupling limit α = π/2 − β. θ
a can be constrained by direct LEP and Tevatron searches for the CP-odd Higgs, but the SM-like higgs could still have large branching fractions to
Za [
4].
 |
(3) |
and the overall size of θ
a does not affect its branching ratios.
For the length of the LHC program it will likely be safe to take
Br(h→
Za)=10% as a benchmark point. In the next section, we discuss the experimental constraints on this mode. Depending on the mass of this pseudoscalar, the dominant decay mode could be
bb, τ
+τ
− or μ
+μ
− (
ss). We consider all of these cases when proposing searching strategies.
Existing Collider Studies
Up to different branching ratios and some angular correlations the final states for
h →
Z ZD and
h →
Z a are identical. As such, collider studies and experimental searches for one channel generally apply to both. The two relevant parameters to define a simplified model for this channel are
 |
(4) |
for
X =
a,
ZD and
y = some SM particle, where the different
a,
ZD branching ratios lend different importance to different choices of
y.
There have not been many collider studies specifically performed for the
h →
Za mode. Ref. [
4] pointed out that this channel may be very large in the context of the NMSSM. Ref [
5,
6,
7] discussed heavy non-SM-like Higgs decaying into
Za.
More searches have been inspired by looking for a
ZD. The phenomenology of a
ZD with mass mixing to the
Z has recently been discussed in [
8,
1,
2,
3] (see also, e.g., [
9,
10,
11,
12] for earlier work), including collider phenomenology of
h→
ZZD,
h→ γ
ZD and
h→
ZDZD decays, as well as low energy constraints from dark photon experiments,
g−2 of the muon, meson physics and electroweak precision observables.
In [
3], the authors designed a search for
pp→
h→
ZZD→
e+e−μ
+μ
−. The backgrounds considered are
Z(→
l+l−)
jj,
j faking
l (probability ∼ 0.1%) and leptonic
tt (reducible), as well as
h→
ZZ*,
Zγ
*,
ZZ and
Z→ 4
l (irreducible). The authors of [
3] assumed only mass mixing of the form ε
Z mZ2 Zμ ZDμ. For
mZD=10 GeV and ε = 10
−6, they find that the luminosity at 14 TeV LHC needed to exclude (2σ), observe (3σ) and discover (5σ) the
ZD is 42, 95 and 260
fb−1, respectively. For half of those values of
mZD and mixing ε
Z the numbers are slightly smaller: (33,75,210)
fb−1.
Existing Searches & Limits
Our focus is the
hZX vertex (
X =
a,
ZD). No direct search for
h →
Za or
ZZD has been performed to be best of our knowledge, but there are several channels and other searches at LEP, Tevatron and LHC that are sensitive to this interaction term.
* LEP
The
hZX vertex not only give rise to the
h→
ZX decay, but also opens the channel
e+e−→
Z* →
h X at LEP. Related searches include
e+ e− →
h a,
ZZ′→ 4
b [
13], 4τ [
13] and 2
b 2τ [
13]. For
Br(h→
Za)=10%, these searches are not constraining because the cross section for
e+e−→
Z* →
h a is at the sub-fb level.
* Tevatron and LHC
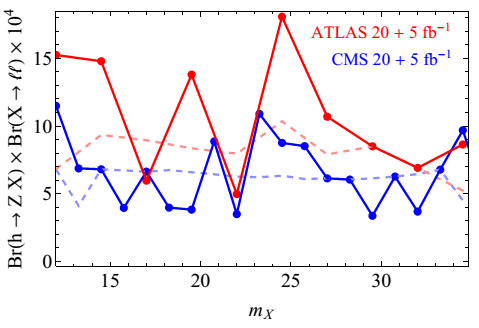
Figure 1: 95% C.L. exclusion limit on Br(h→ Z X)×Br( X→ ll) for X = ZD, a, extracted from the SM h → 4 l searches (l = e, μ) assuming SM higgs production rate and ΓX << 1 GeV. (The lighter dashed lines indicate the expected limit. The large fluctuations in the observed limit are a consequence of low statistics in each bin.)
The most relevant existing search sensitive to
h→
ZZD and
h→
Za is
h→
ZZ* → 4
l by CMS [
14] and ATLAS [
15], where 4
l stands for electrons and muons. The cleanliness of the 4
l decay makes these existing searches very sensitive to
ZZD or
Za decaying into leptons.
The leptonic
h →
ZZ* searches divide the four leptons of each event into two pairs, the "leading" pair (likely to have come from an on-shell
Z) and the "subleading" pair (from the off-shell
Z*). With The subleading dilepton mass distributions from ATLAS and CMS using 20 + 5
fb−1 data set it is easy to estimate limits on
h →
Z X decay. We show our translated 95% CL bounds on this exotic branching fraction for different
mX > 12 GeV in Fig.
1, see
arXiv:1312.4992 for more details.
The bound on
Br(h →
ZX) ×
Br(X →
ll) is <~10
−4 − 10
−3 for 12 GeV <~
mX <~34 GeV and
l =
e, μ. The situation is more ambiguous for pseudoscalars. Their branching ratios are more model-dependent in general, and their Yukawa couplings usually imply that
a → ττ is enormously preferred over
e, μ. Bounds for
X → ττ could also be derived from the leptonic
h →
Z Z* searches but would be much weaker. Nevertheless this may be the preferred discovery channel for
2HDM+S and
NMSSM type models, where
Br(h →
Z a) could easily be 10% and
Br(a → ττ
) is generally
O(0.05-1), see
2HDM+S.
Proposals for New Searches at the LHC
For
ma, ZD > 12 GeV it seems likely that LHC14 searches inspired by
h→
ZZ* will constrain
h →
Za in the
a→ 2τ modes, while LHC7+8 already gives significant
direct bounds to
h →
Z ZD → 4
l. A
Z + lepton jet search would be able to set strong limits in particular for very light
ZD. Care must be taken to correctly account for challenging quarkonium backgrounds. Identifying promising search strategies will be the subject of future work.
Updates
Here we list new experimental and theory results pertinent to this exotic higgs decay channel.
- Adam Falkowski, Roberto Vega-Morales, Exotic Higgs decays in the golden channel, arxiv:1405.1095
References
- [1]H. Davoudiasl, H.-S. Lee, and W. J. Marciano, 'Dark' Z implications for Parity Violation, Rare Meson Decays, and Higgs Physics, Phys.Rev. D85 (2012) 115019, [arXiv:1203.2947].
- [2]H. Davoudiasl, H.-S. Lee, and W. J. Marciano, Dark Side of Higgs Diphoton Decays and Muon g-2, Phys.Rev. D86 (2012) 095009, [arXiv:1208.2973].
- [3]H. Davoudiasl, H.-S. Lee, I. Lewis, and W. J. Marciano, Higgs Decays as a Window into the Dark Sector, [arXiv:1304.4935].
- [4]N. D. Christensen, T. Han, Z. Liu, and S. Su, Low-Mass Higgs Bosons in the NMSSM and Their LHC Implications, [arXiv:1303.2113].
- [5]G. Mahlon and S. J. Parke, Using Spin Correlations to Distinguish Zh from ZA at the International Linear Collider, Phys.Rev. D74 (2006) 073001, [hep-ph/0606052].
- [6]S. Chang and A. Menon, Discovering Nonstandard Higgs bosons in the H→ZA Channel Decay to Multileptons, JHEP 1302 (2013) 152, [arXiv:1211.4869].
- [7]M. M. Almarashi and S. Moretti, LHC Signals of a Heavy CP-even Higgs Boson in the NMSSM via Decays into a Z and a Light CP-odd Higgs State, Phys.Rev. D85 (2012) 017701, [arXiv:1109.1735].
- [8]H. Davoudiasl, H.-S. Lee, and W. J. Marciano, Muon Anomaly and Dark Parity Violation, Phys.Rev.Lett. 109 (2012) 031802, [arXiv:1205.2709].
- [9]A. Hook, E. Izaguirre, and J. G. Wacker, Model Independent Bounds on Kinetic Mixing, Adv.High Energy Phys. 2011 (2011) 859762, [arXiv:1006.0973].
- [10]S. Gopalakrishna, S. Jung, and J. D. Wells, Higgs boson decays to four fermions through an abelian hidden sector, Phys.Rev. D78 (2008) 055002, [arXiv:0801.3456].
- [11]R. Schabinger and J. D. Wells, A Minimal spontaneously broken hidden sector and its impact on Higgs boson physics at the large hadron collider, Phys.Rev. D72 (2005) 093007, [hep-ph/0509209].
- [12]K. Babu, C. F. Kolda, and J. March-Russell, Implications of generalized Z - Z-prime mixing, Phys.Rev. D57 (1998) 6788-6792, [hep-ph/9710441].
- [13]ALEPH, DELPHI, L3, OPAL, LEP Working Group for Higgs Boson Searches Collaboration, S. Schael et. al., Search for neutral MSSM Higgs bosons at LEP, Eur.Phys.J. C47 (2006) 547-587, [hep-ex/0602042].
- [14]Properties of the Higgs-like boson in the decay H to ZZ to 4l in pp collisions at sqrt s =7 and 8 TeV, Tech. Rep. CMS-PAS-HIG-13-002, CERN, Geneva, 2013.
- [15]ATLAS Collaboration, Measurements of the properties of the Higgs-like boson in the four lepton decay channel with the ATLAS detector using 25 fb-1 of proton-proton collision data, ATLAS-CONF-2013-013
File translated from TEX by TTH, version 4.03. On 18 Dec 2013, 11:46.